L’algoritmo di compressione di immagini JPEG e’ stato sviluppato dallo Joint Photographic Expert Group alla fine degli anni ottanta. Per ottenere una immagine compressa questa deve passare attraverso una serie di sotto-algoritmi e strutture dati. L’intero processo crea un file di output con sufficiente informazione da permettere il successivo ripristino dell’immagine compattata.

1. Il primo passo e’ quello di estrarre un blocco di 8x8 pixels dall’immagine originale.
2. Il secondo passo prevede il calcolo della trasformata coseno discreta (DCT) per ogni elemento  del blocco.
3. Una quantizzazione dei coefficienti della trasformata coseno discreta (questa e’ la fase dove la maggior parte del contenuto informativo della immagine e’ perso).
4. I coefficienti quantizzati vengono compressi utilizzando uno schema di codifica come ad esempio la Codifica di Huffman o la cosiddetta codifica Aritmetica.

1.  Il primo passo come abbiamo detto consiste nel raggruppare campioni dell’imagine sorgente in una matrice (o blocco) 8x8 .  Questa matrice sara’ il corrispondente input alla Trasformata Coseno Discreta (DCT).

2. Applicazione della Trasformata Coseno.

La DCT e’ definita nel modo seguente:

 
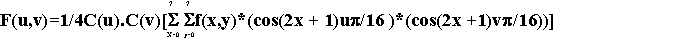Ogni blocco 8x8 di campioni dell’immagine sorgente e’ in effetti un segnale discreto di 64 punti il quale e’ una funzione a due variabili x e y .

 

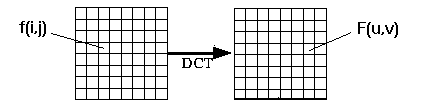La trasformata Coseno Discreta prende il segnale come input e lo decompone in 64 basi ortogonali.

L’output  della DCT e’ un set di 64 ampiezze del segnale base detti “Coefficenti DCT” i cui valori sono univocamente determinati dal particolare punto del segnale  di input. I coefficenti DCT possono essere interpretati come il valore medio delle frequenze spaziali 2D contenute nei 64 punti del segnale di input. Il coefficente con frequenza zero nelle due dimensioni e’ chiamato “Coefficiente DC” ed i rimanenti 63 sono chiamati “Coefficenti AC” . Poiche’ i valori campionati variano lentamente da punto a punto lungo l’immagine, i vari passi del processo della DCT mirano ad ottenere la compressione concentrando la maggior parte del segnale nelle frequenze spaziali basse. Per esempio, in un tipico blocco campione 8x8 di una tipica immagine sorgente, la maggior parte delle frequenze spaziali hanno ampiezza zero o vicina allo zero e non hanno bisogno di essere codificate.

3. Quantizzazione.

Fino a questo punto nel processo JPEG di compressione abbiamo ottenuto una piccola compressione dell’immagine. “Semplicemente” abbiamo  convertito la nostra immagine in una matrice 8x8  di coefficenti DCT. Ora dobbiamo prepare la matrice ottenuta per una ulteriore compressione quantizzando ogni elemento della matrice utilizzando una tabella di quantizzazione. I valori delle costanti della tabella dipenderanno dalla qualita’ di immagine JPEG che si vuole ottenere, la quale e definita dall’utente. Il numero utilizzato per calcolare le costanti di quantizzazione e’ conservato nello header dell’immagine JPEG, rendendo cosi possibile la successiva decodifica. Una volta costruita la tavola le costanti di questa sono utilizzate per quantizzare i coefficenti DCT. Ogni coefficiente DCT e’ diviso dalla corrispondente costante  ed arrotondato al piu’ vicino intero. Il risultato della quantizzazione dei coefficenti DCT  e che meno contano verranno eliminati e  quelli piu’ grandi perderanno precisione non necessaria. Quantizzare produce una lista di coefficenti che possono esssere efficentemente compressi utilizzando sia il metodo di Huffman che quello aritmetico. Come si potra’ notare la quantizzazione e’ un passo essenziale nel processo di compressione JPEG. Non solo l’immagine viene ridimensionata, ma viene persa parte della qualita’ della immagine iniziale. Questo e’ il motivo per il quale la compressione JPEG d’immagini viene chiamata “lossy compression” anche se di solito la perdita d’informazione non e’ percettibile dall’occhio umano .

La formula di quantizzazione e’ definita nel modo seguente:

 

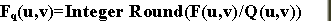4. Codifica Entropica. Prima della codifica vera e propria si deve ordinare la matrice dei coefficenti quantizzati in modo tale che quelli che rappresentano basse frequenze vengano a trovarsi all’inizio della matrice e gli elementi che rappresentano le alte frequenze vengano messi alla fine della matrice. Cosi facendo le alte frequenze (che saranno quasi tutte degli zero) verranno a trovarsi alla fine della matrice creando lunghe sequenze di zeri che permettono una piu’ efficace compressione. Questo  ordinamento viene chiamato a zig-zag , come infatti possiamo notare dalla figura:

 

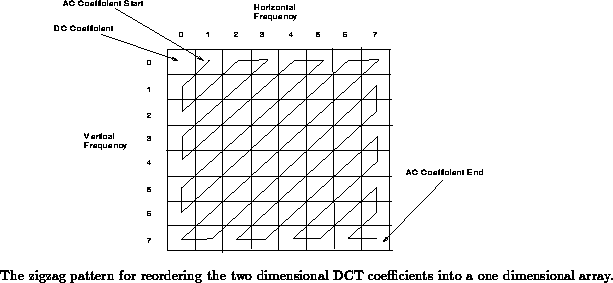Sia lo schema di codifica di Huffman (approccio Baseline) che quello aritmetico (Lempel-Zif-Welsh Algorithm (LZW) ) sono permessi dallo standard JPEG per la compressione finale dell’immagine. Sebbene la codifica aritmetica offra spesso migliori risultati in termini di dimensioni finali del file, questo e’ poco utilizzato poiche’ coperto da copyright dell’ IBM, AT&T e Mitsubishi. Per questo ed altri motivi l’algoritmo di Huffman e’ quello piu’ utilizzato ed e’ quello che sara’ descritto di seguito.

Lo  schema di codifica di Huffman e’stato sviluppato da David A. Huffman nel 1952. Questo algoritmo ottiene la compressione di dati codificandoli in base alla loro frequenza. La struttura di dati utilizzata e’ un albero binario pesato, o Albero di Huffman.

Un albero di Huffman gode delle seguenti proprieta’:

1. E’ un albero binario.
2. E’ pesato; gli elementi che appaiono piu’ frequentemente appaiono nella parte superiore dell’albero, mentre quelli meno frequenti nella parte inferiore o radice dell’albero.
3. Ad ogni ramo sinistro dell’albero viene assegnato il valore zero e ad ogni ramo destro il valore uno (o viceversa).

Algoritmo Basico:

Per costruire un’albero di Huffman i dati devono ancora essere elaborati attraverso due passi che sono:

1. La creazione di una lista degli elementi e della loro frequenza. Questa e’ ordinata in ordine ascendente, quindi mettendo quelli piu’ frequenti alla fine della lista.

2. L’albero di Huffman “attuale” e’ costruito. Si prendono  prima i due elementi di frequenza piu’ bassa e si sommano le loro frequenze. L’albero ottenuto e’ inserito nella lista (l’ordine e’ determinato dal valore di frequenza ottenuto dalla somma) e i due elementi della lista gia’ utilizzati vengono eliminati. Questo procedimento viene ripetuto finche’ nella lista rimane un unico elemento che rappresenta il nodo padre dell’albero di Huffman finale.

Prima che l’albero possa essere utilizzato per codificare i dati si deve stabilire un modo per identificare univocamente ogni valore dell’albero. Questo e’ fatto assegnando ad ogni ramo sinistro dell’albero valore zero e ad ogni ramo destro valore uno. Ora e’ possibile identificare univocamente ogni elemento dell’albero usando sequenze di 0 e di 1 assegnate ad ogni ramo. Una tabella contenente il codice univoco per ogni foglia dell’albero di Huffman e’ generata percorrendo l’albero.

L’ultimo passo che rimane e’ la creazione del file di output contenente le relazioni tra dati originali e codice di Huffman.

Esempio:

Carattere	Frequenza
b	7
d	13
a	17
c	22
g	45
e	77
f	90

Passo 1:

 

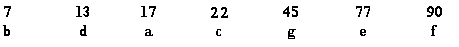Passo 2:

 

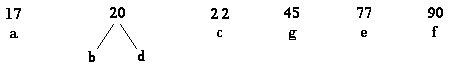Passo 3:

 

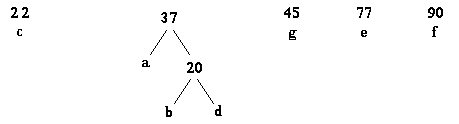Passo 4:

 

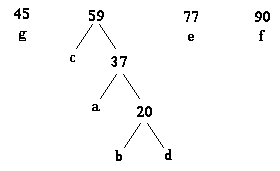Passo 5:

 

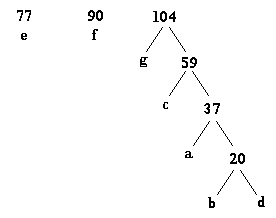Passo 6:

 

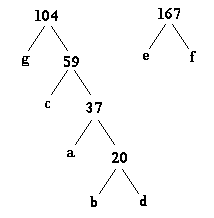Passo 7:

 

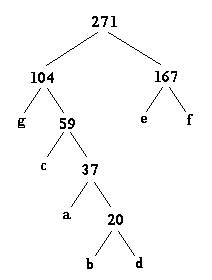Passo 8:

 

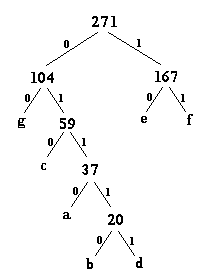Alla fine percorrendo l’albero di Huffman finale dall’alto verso il basso otteniamo:

 

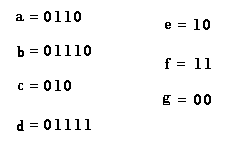Considerazioni Finali:

La compressione delle immagini e’ una parte estremamente importante della informatica moderna, poiche’ offre  la possibilita’ di comprimere immagini ad una frazione della loro dimensione originale, risparmiando considerevolmente lo spazio di memoria necessario per  conservarle. Inoltre, la trasmissione delle immagini da un computer ad un altro diventa molto facile e impiega minor tempo. L’algoritmo di compressione JPEG offre un efficace metodo per comprimere immagini con la minor perdita di qualita’ possibile. Sebbene l’attuale implementazione dell’algoritmo JPEG sia piu’ difficile di altri formati di immagine (vedi GIF) e l’attuale compressione di immagine e costosa in termini computazionali, l’alto rapporto di compressione che puo’ essere ottenuto normalmente utilizzando l’algoritmo JPEG compensa ampliamente l’ammontare di tempo speso per l’implementazione dell’algoritmo e la compressione dell’immagini.

  Riferimenti: